Website founded by
Milan Velimirović
in 2006
1:53 UTC


| |
MatPlus.Net  Forum Forum  General General  Six-fold square vacation by white king Six-fold square vacation by white king |
| |
|
|
|
|
You can only view this page!
| | | (1) Posted by Joose Norri [Tuesday, May 14, 2019 22:32]; edited by Joose Norri [19-05-14] | Six-fold square vacation by white king
In 1942, Veikko Salonen (1919-1992) published this, which is in FA 1914-44, P1055898. (The source there is wrong.) It shows six white square vacations by the white king (threat inclusive) and four variations are bi-valve. The 1...Ne2 variation is an obstruction, I suppose, although also a line injury, if you allow.
 (= 6+13 ) (= 6+13 )
3#; Aamulehti 15.3.1942, 3rd pr. SSL 1938-42 (must have been a ring tourney)
The position is not so pleasing to the eye and the key (1.Ne8! threat 2.Kd8) brings the out of play knight into play, but is there a better six-fold rendition?
He had published earlier versions, P1223761, Tidskrift för Schack, 2nd pr. 1936, and yacpdb 462296. It's interesting to see how a not-too-great a composer gradually worked his way up to the best that he could find.
| | | (2) Posted by Branislav Djurašević [Wednesday, May 15, 2019 11:56] |
It is necessary to say this problem presents complete duel between white King and black knight, so this fact raises the value of the problem itself.
| | | (3) Posted by Petko Petkov [Wednesday, May 15, 2019 16:42] |
A very nice problem but the construction is not optimal. If we put a white Rook on b7, we can remove Bb8 and Pa7 (5+13 pieces, C+).
| | | (4) Posted by seetharaman kalyan [Wednesday, May 15, 2019 18:12] |
Superb problem. Surprising the obvious improvement was missed. Kudos to master Petkov for noticing it immediately.
| | | (5) Posted by Joost de Heer [Wednesday, May 15, 2019 23:23] |
Depends on your definition of economy. E.g. in the reconstruction column in Probleemblad, a white pawn(2)+bishop(4) is cheaper than a white rook(7).
| | | (6) Posted by Hauke Reddmann [Thursday, May 16, 2019 10:40] |
@Petko: My immediate idea too. THX for relieving me from cook checking :-)
What annoys me much more is the Pb6 (no chance to get rid of it, 1...e2!)
and the Pb5 (only protects Pa6 against mobbing).
| | | (7) Posted by Geoff Foster [Friday, May 17, 2019 04:20] |
Here is a similar setting, which was also selected for the FIDE Album.
Nils G.G. van Dijk
2nd Prize, Main Post 1958
 (= 7+14 ) (= 7+14 )
#3
1.e8=S! (>2.Kd8 >3.Sc7)
1...Sg6 2.Kxd6
1...Sf3 2.Kc8 (2.Kxc6?)
1...Sf5 2.Kd7 (2.Kc8?)
1...Sg2 2.Kxc6
1...Be2 2.Kxb6
The final variation is by a different black piece, with White having to allow for 2...Bxa6.
The following one is a bit different.
Antti G. Ojanen
4 Comm, V.Marin y Llovet MT 1942-43
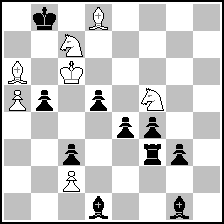 (= 7+10 ) (= 7+10 )
#3
1.Se7! (>2.Kd7 >3.Sc6)
1...Bc5 2.Kxc5
1...Bb6 2.Kxb6
1...Rf1 2.Kxd5
1...Rf2,Re3 2.Kd6
1...Rd3 2.Kxb5
Perhaps the following problem holds the record, with 7 (or 8?) square vacations.
Theodor Siers (in memoriam G.Hume)
British Chess Magazine 1938 (v)
 (= 12+6 ) (= 12+6 )
#3
1.Bf6! (>2.Kxb7 >3.Sc6)
1...Rb8 2.Kd6
1...Ra7 2.Kxc5 Rc7+ 3.Sc6
1...Rxb5 2.Kxb5 (>3.Sc6,Sg6,Sef3,Sec4)
1...Rxd7 2.Kxd7
1...Rc7+ 2.Kxc7
1...Rb6+ 2.Kxb6
1...Bxd5+ 2.Kxd5 f4,fxg4 3.Sc6
The 1...Rxb5 variation does not really feature a square vacation, because 3.Sc6 is not forced.
| |
No more posts |
MatPlus.Net  Forum Forum  General General  Six-fold square vacation by white king Six-fold square vacation by white king |
|
|
|
 ISC 2024
ISC 2024 Forum
Forum  General
General  Six-fold square vacation by white king
Six-fold square vacation by white king