Website founded by
Milan Velimirović
in 2006
23:11 UTC


| |
MatPlus.Net  Forum Forum  Fairies Fairies  My favorite series-mover My favorite series-mover |
| |
|
|
|
|
You can only view this page!
| | | (1) Posted by Dan Meinking [Sunday, Apr 22, 2012 19:21]; edited by Dan Meinking [12-04-22] | My favorite series-mover
This GPS masterpiece was posted on PDB today as P1237311:
George P. Sphicas, 1st Prize, Quartz 2004
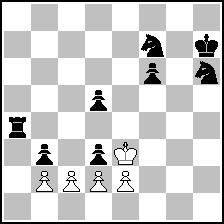 (= 5+8 ) (= 5+8 )
ser-s#30 (5+8) C? ( my assumption; PDB does not indicate C+ )
Solution hidden here:
1. c4 2. Kf4 3. e4 4. cxd5 5. d6 6. d7 7. d8=D 8. Dxd3 9. Dxb3 10. d4 11. e5 12. e6 13. e7 14. e8=S 15. Sg7 16. Dxf7 17. b4 18. d5 19. d6 20. d7 21. d8=L 22. Lxf6 23. Kg5 24. b5 25. b6 26. b7 27. b8=T 28. Tb5 29. Tf5 30. Sh5+ Sxf7#
Most series problems are fairly light on strategy. But here the amazing feat of 4x excelsior + AUW is almost secondary to the breathtaking pin action along the 4th rank. Great economy too. A chessboard miracle!
| | | (2) Posted by seetharaman kalyan [Sunday, Apr 22, 2012 22:50] |
I have seen some very good AUWs in seriesmovers. But nothing to compare to this - the best, a masterpiece. All four white pawns get pinned on the fourth rank and wait to be unpinned before promoting. Really spectacular!!
| | | (3) Posted by Arno Tungler [Tuesday, Aug 25, 2015 12:42] |
I agree with the late Dan Meinking that this is a great seriesmover! However, I also would like to show my favorite here, also with a promotion task and a stunning motivation for the move order.
Zdravko Maslar
5722v feenschach 1989
1st Prize
 (= 14+8 ) (= 14+8 )
ser-s=34
1.d8=B 2.d7 3.d6 4.d5 5.Sd4 6.Se6 7.exf8=B 8.Bh6 9.f8=B 10.f7 11.Bh4 12.d8=B 13.d7 14.d6 15.Kd5 16.Sg5 17.Sh7 18.Bdg5 19.d8=B 20.d7 21.Rg6 22.a6 23.axb7 24.b8=B 25.Bbe5 26.Bh8 27.Bfg7 28.f8=B 29.Rf7 30.Bdf6 31.d8=B 32.Bde7 33.Ke5 34.Qc4+ Kxc4=
Probably you will only be able to understand my excitement for the problem if you solve it yourself - as I did in 1989 - without knowing what the author had planned. The idea of trying bishop promotions came after some time but then, how this can have a unique move-order?? With rook promotion that is "so easy" but bishops...? My comment in the solutions for the original cooked problem was then: "What should we say to that? A terrific idea in indescribable elegant design with a brilliant solution-mechanism that almost entirely dispenses with the usual blocking units in seriesmovers. A piece that makes you think of ceasing composition activity as anyhow such composing height seems out of reach. A perfect problem, even not spoiled by the cook as this seems easily avoidable (my today's translation from German). I still agree...
| |
No more posts |
MatPlus.Net  Forum Forum  Fairies Fairies  My favorite series-mover My favorite series-mover |
|
|
|
 ISC 2024
ISC 2024 Forum
Forum  Fairies
Fairies  My favorite series-mover
My favorite series-mover