|
|
| (1) Posted by Eric Huber [Saturday, Jul 19, 2014 19:02] |
12th Tzuica Tourney
This year's theme is : helpselfmates with at least two solutions where mate is given by double check.
All fairy pieces and conditions are accepted, provided that the problem can be checked by a known solving program.
Mates by triple check, quadruple check and so on are accepted.
Deadline: August 24th by email hubereric@yahoo.fr, August 27th at Bern congress.
As usual, prizes in bottles of Tzuica.
Details and examples can be found in the PDF file here: https://drive.google.com/file/d/0B2R4SBE7r8AtN19UTkRScGgtXzg/edit?usp=sharing
Good luck to all !
Example 1 for Orthodox section
Vlaicu Crişan
6578, Phénix 222/2012
dedicated to Denis Blondel
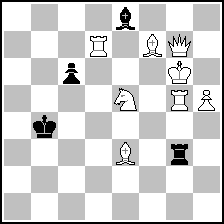 (= 8+4 ) (= 8+4 )
hs#4 ( 8 + 4 )
b) bPc6->d3
A: 1.Bc1 Ra3 2.Re7 Ra6 3.Sxc6+ Bxc6 4.Re4+ Bxe4#
B: 1.Ra7 Ba4 2.Bf4 Bc2 3.Sxd3+ Rxd3 4.Bd6+ Rxd6#
Example 2 for Fairy section
Vlaicu Crişan & Eric Huber
Prize, Quartz TT6 2004
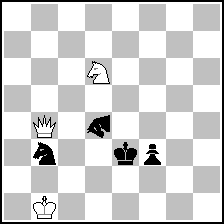 (= 3+4 ) (= 3+4 )
hs#3 2 sol. ( 3 + 4 )
Augsburg, Circe
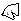 = (R+S) = (R+S)
1.Qd6(=Q+S) Sc5 2.Kc1 (R+S)c6 3.(Q+S)d3+ Sxd3(+wQd1,+wSb1)#
1.Rxd4(Bb4;+wRh8,+bSb8) Rb8=(R+S) 2.Rd2 (R+S)xb4(+wBc1) 3.Bd2=(B+R)+ Sxd2(+wRa1,+wBc1)#
|
|
| (2) Posted by Diyan Kostadinov [Sunday, Jul 27, 2014 00:56] |
Eric, Vlaicu, I not remember - problems with orthodox pieces but with fairy condition - in which section they are?
|
|
| (3) Posted by Eric Huber [Sunday, Jul 27, 2014 17:02] |
Problems with orthodox pieces but with fairy condition, as well as problems with fairy pieces and without fairy condition, all compete in the Fairy Section.
By the way, "2 solutions" means that twins are allowed as well.
|
|
| (4) Posted by Nikola Predrag [Sunday, Jul 27, 2014 17:43]; edited by Nikola Predrag [14-07-27] |
I tried to conclude from the solutions what is Augsburg. It seems almost clear but for the rebirth of white Rh8.
Is it a typo (or Augsburg is much more complicated than I can guess)?
|
|
| (5) Posted by Eric Huber [Sunday, Jul 27, 2014 18:42] |
Nikola, thank you very much for spotting the typo ! Indeed it should read +bRh8 instead of +wRh8.
You must have guessed how Augsburg condition works. The definition of Augsburg can be found on Problemesis website:
http://christian.poisson.free.fr/problemesis/condra.html#Augsburg
"A unit (except a King) can move on a square occupied by a piece of its side.
All the pieces on a square keep their power.
When one of these pieces moves, the other ones can follow it or stay. "
|
|
| (6) Posted by Nikola Predrag [Monday, Jul 28, 2014 00:46]; edited by Nikola Predrag [14-07-28] |
Thanks Eric, I guess that Q=R+B as default. Is it so with Grasshopper, Contra-Grasshopper, Kangaroo, Lion, Leo, Locust, Sirene or whatever else?
What about the Chameleons?
|
|
| (7) Posted by Joost de Heer [Monday, Jul 28, 2014 08:27] |
Q is almost, but not quite R+B. A queen may split itself into a R+B, but when captured it is reborn as a queen, whereas a R+B is reborn as a R and a B (see second solution).
|
|
| (8) Posted by Nikola Predrag [Monday, Jul 28, 2014 09:34] |
Hm, Queen can split itself into R+B. When these particular parts join together again, can they ever make the original Queen which would be reborn as the Queen? Would a simple switchback make the original wQ e.g. 1.Rc4 and 2.Rb4=(Q)?
Or a Q once split, can never become Q again?
Are there precise rules somewhere?
(In the second solution, wBc1 is reborn and it's not exactly the same part of the original wQ as it was wBb4, so 3.Bd2=(B+R) doesn't make wQ.)
|
|
| (9) Posted by Eric Huber [Monday, Jul 28, 2014 21:49] |
In fact Q and (R+B) are 2 different units in Augsburg+Circe, because they are reborn differently when captured. However, they are represented by the same symbol on the board. In the problem diagram, you initially don't know whether the piece standing on b4 is Q or (R+B).
During one solution the unit is revealed to be either Q or (R+B) but it cannot be both consecutively, that would not be consistent.
In 2004 the problem was presented with two twins: A) wQb4 and B) w(R+B)b4 in order to avoid any kind of misunderstanding.
The 6th TT organized by Quartz magazine in 2004 was dedicated to problems with conditions Augsburg + any kind of Circe.
|
|
| (10) Posted by Eric Huber [Friday, Aug 29, 2014 19:32] |
The prizes were given today during the prize giving ceremony at Berne.
The award of the 12th Tzuica Tourney is published on the Internet (I know nothing of the Congress Bulletin)
https://drive.google.com/file/d/0B2R4SBE7r8AtVXpMVjZlODJLOEk/edit?usp=sharing
|
|
| (11) Posted by seetharaman kalyan [Friday, Aug 29, 2014 21:05] |
Great Problems! Some amazing ones with very few pieces.... eg. Tadashi Wakashima's 3rd Commend. !
|
|
| (12) Posted by Eric Huber [Saturday, Aug 30, 2014 09:04] |
The economy record is Cornel Pacurar's 4th prize with only 4 pieces and 4 solutions. But of course Tadashi Wakashima's problem is very pleasant and elegant.
For those interested, the congress bulletin has been published: http://www.kunstschach.ch/wccc2014/docs/WCCC2014_Berne_Booklet.pdf
|
|
| (13) Posted by shankar ram [Wednesday, Sep 3, 2014 16:22] |
Eric.. Where can I get to see the awards of ALL the Tzuica tourneys..?
|
|
| (14) Posted by Eric Huber [Wednesday, Sep 3, 2014 19:28] |
All Tzuica Tourney awards are available on the ChessComposers blog:
http://chesscomposers.blogspot.com/p/tzuica-tourney.html
|
|
| (15) Posted by shankar ram [Thursday, Sep 4, 2014 04:45] |
Great..! Thanks..
|
|
| (16) Posted by Eric Huber [Thursday, Sep 4, 2014 20:58] |
Well, thank you for your question : it made me realize that the Tzuica awards can be found only on WCCC websites (which are not always long-lived) and on the website of the Romanian Chess Federation (which not many non-Romanians have heard of).
Hopefully the webpage with all Tzuica awards and themes will prove useful.
|
|
No more posts |
MatPlus.Net  Forum Forum  Competitions Competitions  12th Tzuica Tourney 12th Tzuica Tourney |
 ISC 2024
ISC 2024 Forum
Forum  Competitions
Competitions  12th Tzuica Tourney
12th Tzuica Tourney