|
|
| (1) Posted by David Knezevic [Monday, Dec 25, 2006 12:00] |
Yet Another Quaternary Correction (#2)
This was one of my experiments in my beloved Correction Play:
Milan Velimirović
3rd Prize BCM 1976 (v) (= 9+9 ) (= 9+9 )
#2*v... | 1... Rb4 2.Qc3#
1... fe3 2.Rd4#
1.K~? (~)
1... Rb3!
1.Kc4!? (~)
1... Rb3 2.Sb3:#
1... Rb4+! (2.Qc3? (Sic!))
1.Kd4!!? (~)
1... Rb3 2.Sb3:#
1... Rb4+ 2.Bb4:#
1... Rb5: 2.Qc3#
1... fe3! (2.Rd4?)
1.Ke4!!! (~)
1... Rb3 2.Sb3:#
1... Rb4+ 2.Bb4:#
1... fe3 2.Be3:#
1... Rb5: 2.Qd4#
1... g2 2.Rg2:# |
The original was published without BPh2 just because, as a very young composer at that time, I was afraid to be critisized for unnecesary piece on the board. This pawn is in fact crucial for thematical purity of the idea, since, with imobilized WRh1, the only remaining way to repeat the set play (and underline the initial weakness of white: no mate for 1... Rb3) are the WK moves, i.e. 1.K~? and three corrections with primary error in WK stepping to the checking line.
|
|
| (2) Posted by seetharaman kalyan [Thursday, May 20, 2010 15:20]; edited by seetharaman kalyan [10-05-21] |
wonderful problem. A masterpiece. Quaternary in twomovers, are there others?
|
|
| (3) Posted by David Knezevic [Thursday, May 20, 2010 16:05] |
There are several examples and, to my opinion, the best one is:
Hrvoje Bartolović
4.e.E. Die Schwalbe 1955
Album FIDE 1945-55, No.342
 (= 8+12 ) (= 8+12 )
#2* vvv |
*1... Bb5,Re8 2.Qxb4,Qd4#
1.Sc1? ~ 2.Qe2#
1... Sf3!
1.Sc3!? ~ 2.Qe2#
1... Sf3 2.S3e4#
1... Bb5!
1.Sd4!!? ~ 2.Qe2#
1... Sf3,Bb5 2.Sxf3,Sdxb3#
1... Re8!
1.Sf4!!! ~ 2.Qe2#
1... Sf3,Bb5,Re8 2.Se4,Sxb3,Qd7# |
|
|
| (4) Posted by Sathya Narayanan [Friday, May 21, 2010 11:17] |
An excellent problem! These correction problems require a total of eight mates spread over 4 phases including the random.Here is an example of mine,obviously of lesser merit, b'cause it has one mate less but it is one of my well constructed problems on the theme which I want to share with my friends.The subtle battery threat, the by-play 1...Be4/ Rg5 2.Be6/Qf7 naturally embedded ,the white pawn-less construction and overall economy are the plus points here.
in Forsyth
8; 3pb1r1; 1s3R1p;1K1kSB1Q; 2p2B2; 4p3;2S3b1;5s2 (10+7)
Strategems 1998
_____
Diagram added by Administrator:
 (= 7+10 ) (= 7+10 )
|
|
| (5) Posted by Jacques Rotenberg [Monday, May 24, 2010 19:47] |
Yes, very nice !
1.S~?[2.Bg6‡] 1…B×f6!
1.Sg6? [2.Bd3‡] 1…B×f6!
1.Sd3!? [2.Bg6‡]
1…B×f6 2.Sdb4‡
1…Sg3!
1.Sf3!!? [2.Bg6‡]
1…B×f6 2.Sb4‡
1…Sg3 2.S×é3‡
1…Bh3!
1.Sg4!!! [2.Bg6‡]
1…B×f6 2.S×f6‡
1…Sg3 2.Sg×é3‡
1…Bé4 2.Bé6‡
1…Bd6 2.R×d6‡
1…R×g4,Rg5 2.Qf7‡
The random move here and in the previous pb is slightly more complex than needed
|
|
| (6) Posted by Kevin Begley [Monday, May 24, 2010 20:53] |
All 3 problems are fantastic -- I'd like to see more!
Including selfmates/reflexmates/fairies (especially if limited fairy elements are employed)...
|
|
| (7) Posted by Juraj Lörinc [Monday, May 24, 2010 21:58] |
Then what about fairy reflex mate?
http://jurajlorinc.tripod.com/chess/m151_156.htm#uloha4
Well, it is not quaternary white correction, just tertiary (as far as I understand the motivation analysis and terminology), but it is enough fairy, enough reflex, all in all, personally I like it a lot (my rating A). Worth of setting up in fairy section?
|
|
| (8) Posted by Jacques Rotenberg [Tuesday, May 25, 2010 00:35] |
Also
http://www.matplus.net/pub/start.php?px=1274740038&app=forum&act=posts&fid=xshow2&tid=87
see specially note 13
|
|
| (9) Posted by Kevin Begley [Tuesday, May 25, 2010 12:58]; edited by Kevin Begley [10-05-25] |
Thanks Juraj & Jacques.
I must admit, I'm not entirely certain that I understand corrections...
I found the following at theproblemist.org, said to be a "A wonderfully clear example of quaternary correction."
Michel Caillaud
2nd HM Lytton 70JT 2009-10
 (= 10+5 ) (= 10+5 )
#2 Circe
1.Qg8! [> 2.Txf7#]
1…S~ 2.Qc4#
1…Sxd6(Sg1) 2.Rf3#
1…Sxg5(g2) 2.Bç1#
1…Sxe5(e2) 2.e3#
This is wonderfully clear, and enjoyable, except that I do wonder where to place the double, triple, and quadruple exclamation-marks.
Have I wandered into that territory where philosophical debates rage about what constitutes a correction?
Is there any formal agreement on what constitutes a correction?
And, why do I get the feeling that the ordering of the solution has an impact upon the degree of correction?
|
|
| (10) Posted by Juraj Lörinc [Tuesday, May 25, 2010 14:27] |
From my viewpoint the text at http://www.bstephen.me.uk/bcps/problemist.html#(49) sums perfectly the motivation chain:
"The thematic key occupies g8 to threaten 2.Rxf7 by preventing the knight’s rebirth. A random move of the unpinned S opens the line g8-c4. 1…Sxd6 corrects by guarding the fourth rank, but places a white guard on f3 for 2.Rf3. 1…Sxg5 again guards the fourth rank and places a white guard on f3 but corrects by directly guarding f3. However, it cuts the rook guard of d2, allowing 2.Bc1. 1…Sxe5 repeats all of the preceding elements but corrects against 2.Bc1? because of 2…Sxd3[Pd2]! This time the decisive error is to return the wP to e2 for 2.e3. A wonderfully clear example of quaternary correction."
What is important, it is repeated presence of the 'same' defence motifs and errors in graded defences. And it is here, masterpiece!
|
|
| (11) Posted by Jean-Marc Loustau [Tuesday, May 25, 2010 15:33] |
A little detail…
Juraj, what is important to make the 4th degree black correction, it is the repeated presence of the 'same' errors in graded defences. The fact there is a repetition of the defence motifs is not mandatory (for example, here the fact Sxg5 and Sxe4 prevent 2 Rf3 for the same motif, the direct control of f3, is not mandatory, it could be different motifs).
Even I would say that different defence motifs (which in fact are anti-dual motifs) are sometimes welcome, as there is more variety in the whole problem… But of course it depends; sometimes the repeated anti-dual motifs are also welcome…
By the way, all the previous problems are excellent!
|
|
| (12) Posted by Kevin Begley [Tuesday, May 25, 2010 17:10]; edited by Kevin Begley [10-05-25] |
I do agree that Michel's problem is lovely.
And, I do understand the logic of calling it a "Quaternary Correction."
However, the theme is actually entirely different from the orthodox examples, where the solution has the following form:
1.tryA?
but 1...a!
1.tryB!?
1...a 2.A1#
but 1...b!
1.tryC!!?
1...a 2.A2#
1...b 2.B1#
but 1...c!
1.KeyD!!!
1...a 2.A3#
1...b 2.B2#
1...c 2.C1#
Shouldn't this be considered a separate thematic classification?
Furthermore, is there any example (orthodox or otherwise) where A1 != A2 != A3, and B1 != B2 (that is to say, all mates change)?
|
|
| (13) Posted by Juraj Lörinc [Tuesday, May 25, 2010 18:18] |
Ah, I see... the problem seems to be in fact that while above given orthodox examples as well as your scheme show/describe white correction, Michel's problem shows black correction. :-)
|
|
| (14) Posted by Kevin Begley [Tuesday, May 25, 2010 21:27] |
Aha! Thanks again, Juraj.
So, white correction appears more challenging... no?
|
|
| (15) Posted by Jacques Rotenberg [Wednesday, May 26, 2010 22:25] |
Another very wellknown problem.
Only third degree white correction, but... twice ! And with diagonal/orthogonal echo.
Alex Casa
Problem 1967
1st Prize
 (= 11+12 ) (= 11+12 )
2#
1.Se~? (1.Sf6?) [2.Qe4‡] but 1…Bf3!
1.Sc5!? [2.Qe4‡]
1…Bf3 2.S×d3‡ but 1…R×c4!
1.Sd6!!? [2.Qe4‡]
1…Bf3 2.S×f3‡
1…R×c4 2.S×c4‡ but 1…Qd4!
a 3rd degree correction couple of tries on a diagonal line (with interference of a wB)
1.S×g5!? [2.Qe4‡]
1…Bf3 2.Sg×f3‡ but 1…Sf6!
1.Sg3!!? [2.Qe4‡]
1…Bf3 2.S×f3‡
1…Sf6 2.Sg6‡ but 1…f3!
a 3rd degree correction couple of tries on an orthogonal line (with interference of the wQ on R-line)
1.Sf2! [2.Qe4‡]
1…Bf3 2.S×d3‡
1…R×c4 2.Bd6‡
1…Qd4 2.e×d4‡
1…Sf6 2.Q×g5‡
1…f3 2.Qg3‡
|
|
| (16) Posted by Sathya Narayanan [Thursday, May 27, 2010 09:04] |
Here is a near perfect example with clear random move unlike in other examples with 8 mates- with a start 1…Sc2? The double threat is the only weakness.
C.G.S.Narayanan
The Problemist 1989 (v)
Forsyth notation
4s3; 3p4; R5Sp; pP1k4; rqRSpp2; 1B1p3s; 5B1K; 3Q1b2(9+12)
1.S any ? (2.Rc5/Rxb4) Qxc4!
1.Sf5? 1…Qxc4 2.fSe7 but 1…Sxf2!(Qh5?)
1.Sf3? 1….Qxc4/Sxf2 2.gSe7/gSxf4 but 1…e3! (2.Qf3?)
1.Se2!! 1….Qxc4/Sxf2/e3 2.Sc3/eSxf4/Qxd3
|
|
| (17) Posted by Jacques Rotenberg [Thursday, May 27, 2010 11:51]; edited by Jacques Rotenberg [10-05-27] |
The diagram :
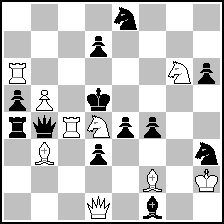 (= 9+12 ) (= 9+12 )
2#
|
|
| (18) Posted by Jacques Rotenberg [Friday, May 28, 2010 00:21] |
see also :
http://www.matplus.net/pub/start.php?px=1274998698&app=forum&act=posts&fid=gen&tid=471
|
|
No more posts |
MatPlus.Net  Forum Forum  Twomovers Twomovers  Yet Another Quaternary Correction (#2) Yet Another Quaternary Correction (#2) |
 ISC 2024
ISC 2024 Forum
Forum  Twomovers
Twomovers  Yet Another Quaternary Correction (#2)
Yet Another Quaternary Correction (#2)